Keywords
Babylonian mathematics, geometry, problem text.
The school text CUNES 52-2-43 gives the solution to a geometric exercise which is to compute the circumferences and the areas of the annuli defined by a system of eight concentric circles. It therefore probably shows a pupil’s sketchy solution of an assignment as it is known from a number of problem texts.
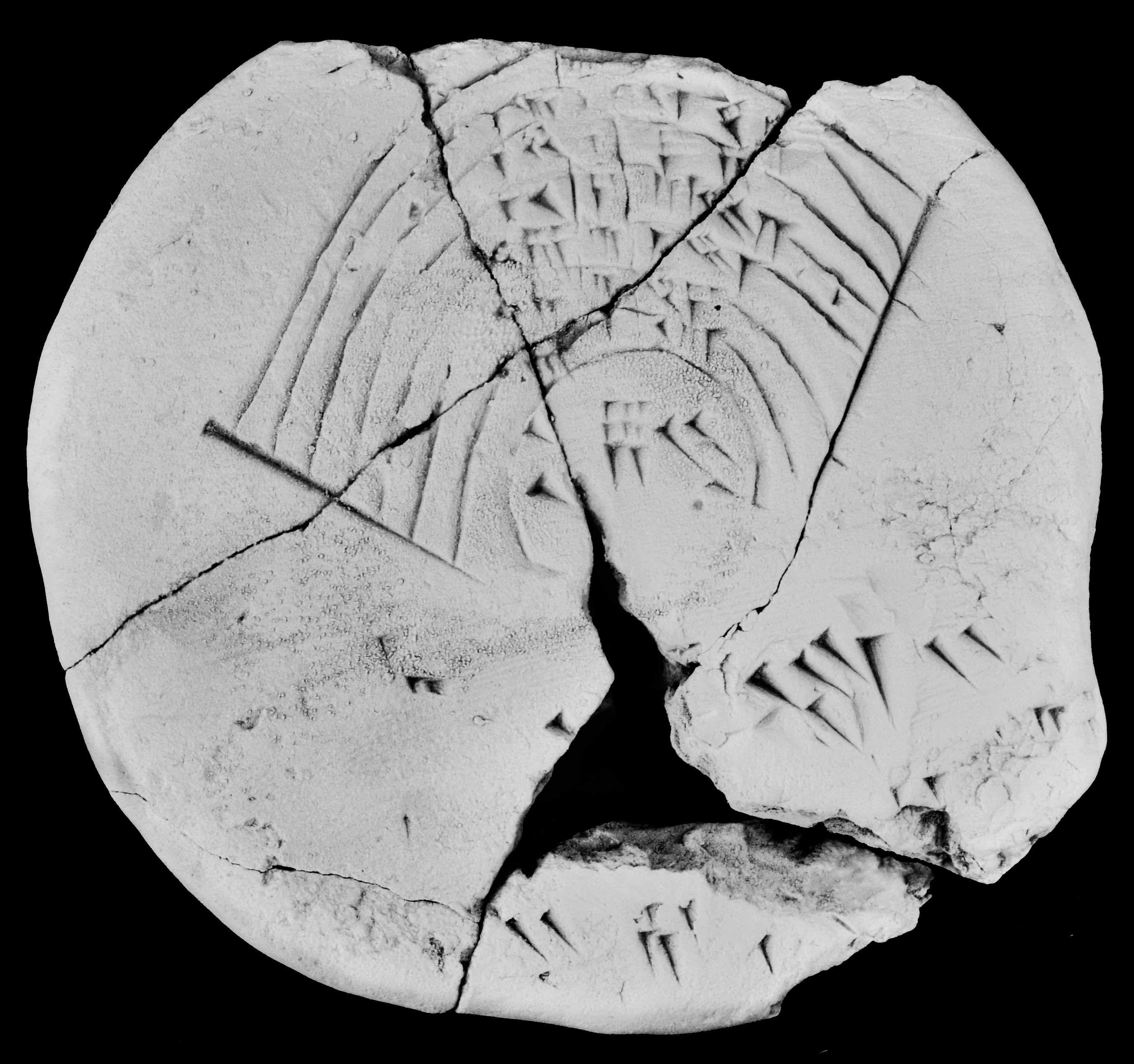
Figure 1: CUNES 52-2-43 obv. Photograph by Laura Johnson-Kelly.
Figure 2: Schematic transliteration of the drawing on CUNES 52-2-43 obv.
The obverse of the lentil-shaped school tablet CUNES 52-2-43 (90×92×32mm; reverse empty, provenience unknown) shows the solution to a geometric exercise dealing with a system of eight concentric circles (figs. 1 and 2). It consists of a scetchy drawing with inscribed numbers representing various length and area values. The drawing depicts only a sector-shaped section of the figure involved and is highly out of scale. In fact, though the annuli bounded by the subsequent circles increase in width by one at each step (see fig. 3), the circles are drawn equidistantly. In the following I will use the symbol π̂ (with value 3) to denote the Mesopotamian equivalent to our π.[1] The numbers given are one possible interpretation. Statements remain valid when at the same time numbers representing lenghts are multiplied by 60k , and those representing areas by 602k for arbitrary integer k.
The interpretation is the following. The innermost circle (“circle 0” in the following) has the area A0 = 08; 20 from which its circumference c0 and radius r0 result as
The circumference c0 seems to be written twice at the left side inside the inner circle. The seven outer circles will be referred to as “circle 1, circle 2, . . .”, in the order of increasing diameter. As indicated by the numbers in the central “column” of the drawing, the widths of the annuli bounded by the subsequent circles (i.e., the increments of the circles’ radii) are ∆i = i (1 ≤ i ≤ 7), i.e. increase arithmetically from inside to outside, whence radius rn and circumference cn of circle n (1 ≤ n ≤ 7) are[2]
and
The area Ãn of the n-th annulus (bounded by the n-th and (n − 1)-th circle) can either be found by computing the areas An and An−1 of the bounding circles as
and then Ãn = An − An−1, or directly from the circumferences cn and cn−1 as[3]
The numerical values for the circumferences cn of the circles, the radial increments ∆i, and the areas Ãn of the annuli are collected in the following table. These are the respective values written in the left, central, and right column of the drawing. The situation is depicted to scale in fig. 3.
| c1 = | 16 | ∆1 = 01 | Ã1 = | 13 | |||
| c2 = | 28 | ∆2 = 02 | Ã2 = | 44 | |||
| c3 = | 46 | ∆3 = 03 | Ã3 = | 01 51 | |||
| c4 = | 01 10 | ∆4 = 04 | Ã4 = | 03 52 | |||
| c5 = | 01 40 | ∆5 = 05 | Ã5 = | 07 05 | |||
| c6 = | 02 16 | ∆6 = 06 | Ã6 = | 11 48 | |||
| c7 = | 02 58 | ∆7 = 07 | Ã7 = | 18 19 |
Figure 3: The situation of CUNES 52-2-43 obv. drawn to scale
The underlying problem text would most likely have given the central circle’s area 08 20 and the arithmetically increasing sequence of radius increments (∆i)1≤i≤7 and asked for the outer circles’ circumferences and the areas of the annuli.[4] The solution would then start by computing the innermost circle’s circumference and radius (see (1)) and proceed by computing the radii of the outer circles (either by successive addition of the radius increments ∆i or by means of (2)) and their circumferences (3). Finally, the areas of the annuli are determined, probably by means of (4) as it is done in W 23291-x, § 2 (Friberg, Hunger & al-Rawi 1990: 494-496), see below.
There are three problems (all accompanied by drawings) that are sort of “complementary” to this one, in that given and asked data are partially exchanged:
- W 23291,x §2 (Friberg, Hunger & al-Rawi 1990: 494-496): Five concentric circles. The problem gives the circumference of the outer circle and a constant radius decrement for the four inner circles (both given as well in the statement of the problem as in the drawing), and asks for the areas of the annuli and the inner circle. As established by Friberg, Hunger & al-Rawi (1990: 495), first the diameters and the circumferences of the inner circles are computed (both denoted only in the drawing) and from those the lengths of the “middle arcs” of the annuli as mean values of subsequent circumferences (given in the text, but not in the drawing). From those and the (constant) radius decrement the areas of the annuli (given in both text and drawing) are computed by means of (4).
- W 23291,x §3 (Friberg, Hunger & al-Rawi 1990: 499-502): Five concentric circles. Given are the diameter of the inner circle and the widths of the annuli. Computed are their areas.
- LB 1821 (Friberg & al-Rawi 2016): Two concentric circles. The problem gives the width ∆ and the area à of the annulus (which in the drawing is written inside the inner circle) and asks for the dimensions of the two circles. First the area of the annulus is divided by π̂∆ to obtain
. Then the radius increment ∆ is first added to this r2 + r1 to obtain r2 + r1 + r2 − r1 = 2r2 = d2 and then subtracted from it to obtain r2+r1−(r2−r1) = 2r1 = d1 with d1, d2 the respective circles’ diameters. From this the circles’ areas are computed.
There are some more signs on the tablet below the drawing which may or may not be connected to the problem of the concentric circles. On the right side immediately below the drawing there is clearly discernible 41 20 next to damaged surface. The area A6 of the sixth circle (not annulus) is 25 41;20, but this need not mean anything.
Notes
|
* I would like to thank Professor David I. Owen, Curator of Tablet Collections, for bringing this tablet to my attention, encouraging its publication, and for arranging for the excellent photo by Laura Johnson-Kelly. This study was done while I held a research position at the Excellence Cluster 264 TOPOI “The Formation and Transformation of Space and Knowledge in Ancient Civilisations.” 1 Purists and those afraid of “anachronisms” won’t like that but it is practical and does no harm. 2 Note that the equality 3 This follows by Because of cn = 10 + 3n(n + 1) the Ãn satisfy 4 The wording would have started with something like “08 20: a circle I have bent” (gur2 akpup). See e.g. New MCT §9.1 LB 1821 (Friberg & al-Rawi 2016); CT 9, plts. 8-13 BM 85194 § 4 (Neugebauer 1935: 144, 153, 167-172): ak-pu-up. BagM 21, 554-557 + plts. 46-47 W 23291,x §§2-3 (Friberg, Hunger & al-Rawi 1990: 494-496, 499-502): gur2up. |
Bibliography
| Friberg, Jöran | ||
| 1987-1990 | “Mathematik.” RlA 7, 531-585. | |
| Friberg, Jöran & al-Rawi, Farouk N. H. | ||
| 2016 | New Mathematical Cuneiform Texts. New York: Springer | |
| Friberg, Jöran, Hunger, Hermann & al-Rawi, Farouk N. H. | ||
| 1990 | “‘Seed and Reeds’, a Metro-mathematical Topic Text from Late Babylonian Uruk.” BagM 21, 483-557 + plts. 46–48. | |
| Neugebauer, Otto | ||
| 1935 | Mathematische Keilschrifttexte I. Berlin: Springer. | |
| Robson, Eleanor | ||
| 1999 | Mesopotamian Mathematics, 2100-1600 BC. Technical Constants in Bureaucracy and Education. OECT 14. Oxford: Clarendon Press. | |
Version: 15 September 2018


